 |
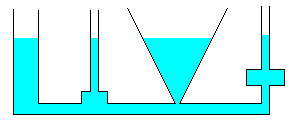
Si se ponen en comunicación varias vasijas de formas diferentes, se observa que el líquido alcanza el mismo nivel en todas ellas. A primera vista, debería ejercer mayor presión en su base aquel recipiente que contuviese mayor volumen de fluido. |
La fuerza debida a la presión que ejerce un fluido en la base de un recipiente puede ser mayor o menor que el peso del líquido que contiene el recipiente, esta es en esencia la paradoja hidrostática.
Como se ha demostrado, en la ecuación fundamental de la estática de fluidos, la presión solamente depende de la profundidad por debajo de la superficie del líquido y es independiente de la forma de la vasija que lo contiene. Como es igual la altura del líquido en todos los vasos, la presión en la base es la misma y el sistema de vasos comunicantes está en equilibrio.
Vamos a examinar en esta página tres ejemplos, dos simples y uno algo más complejo para explicar esta paradoja.
En todos los casos, hemos de tener en cuenta que la fuerza que ejerce un fluido en equilibrio sobre una superficie debido a la presión es siempre perpendicular a dicha superficie.
Recipientes de forma cilíndrica
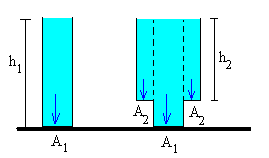 |
Primer ejemploConsideremos dos recipientes con simetría cilíndrica, ambos contienen líquido hasta la misma altura h1. |
Recipiente de la izquierda
- Peso del líquido
El peso del líquido contenido en el recipiente de la izquierda de forma cilíndrica es
m1g=ρA1h1g
- Fuerza debida a la presión en sus bases.
La presión que ejerce el líquido en la base es
P= ρh1g
La fuerza debida a la presión es
F=PA1= ρA1h1g
En el recipiente de la izquierda, ambas cantidades coinciden.
Recipiente de la derecha
- Peso del líquido
El peso del líquido contenido en el recipiente de la derecha es la suma del peso del líquido contenido en el cilindro de base A1 y altura h1, y del cilindro hueco de base anular A2 y altura h2.
m2g= ρA1h1g+ ρA2h2g
- Fuerza debida a la presión en sus bases.
El líquido ejerce una fuerza hacia abajo en su base A1 debida a la presión
F1= ρA1h1g
También ejerce una fuerza en su base anular A2 debida a la presión del líquido situado encima,
F2=ρA2h2g
Ambas fuerzas tienen el mismo sentido, hacia abajo. La resultante es igual al peso del fluido
F1+F2=m2g
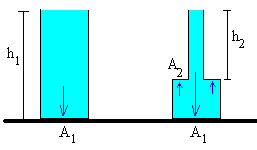 |
Segundo ejemploComparamos ahora estos otros dos recipientes |
Recipiente de la izquierda
- Peso
El peso del líquido contenido en este recipiente es
m1g=ρA1h1g
- Fuerza debida a la presión en sus bases.
La presión en la base del recipiente es
P= ρh1g
La fuerza debida a esta presión es
F=PA1= ρA1h1g
Ambas cantidades coinciden.
Recipiente de la derecha
- Peso
El peso del líquido contenido en el recipiente de la derecha es la diferencia entre el peso del líquido contenido en el cilindro de base A1 y altura h1, y el peso del líquido contendido en el cilindro hueco de base anular A2 y altura h2.
m2g= ρA1h1g- ρA2h2g
- Fuerza debida a la presión en sus bases.
El líquido ejerce una fuerza en la base A1 debida a la presión del líquido que está encima, y es igual a F1= ρA1h1g, apuntando hacia abajo
También ejerce una fuerza en su base anular A2 debida a la presión del líquido situado encima, igual a F2=ρA2h2g pero en sentido opuesto
La resultante nos da el peso del líquido contenido en el recipiente.
F1-F2=m2g
Como vemos, la paradoja queda resuelta si consideremos la fuerza que ejerce el fluido debido a la presión en la superficie anular A2, que en el primer ejemplo es hacia abajo y en el segundo es hacia arriba.
Hemos comprobado en dos ejemplos sencillos que la suma de las fuerzas verticales debidas a la presión que ejerce el fluido en las paredes del recipiente iguala al peso del fluido contenido en el mismo.
Recipiente de forma cónica
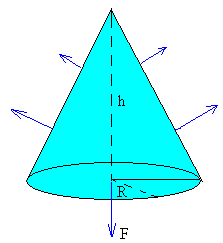
Sea un recipiente en forma cónica, de altura h, cuya base tiene un radio R y que está completamente lleno de líquido.
 |
El peso del líquido de densidad ρ es
La fuerza hacia abajo que ejerce el líquido en su base debido a la presión es F=ρgh(πR2) que es el triple del peso del líquido contenido en el cono |
La paradoja se resuelve considerando todas las fuerzas que ejerce el líquido debido a la presión en la superficie cónica y que son perpendiculares a la misma.
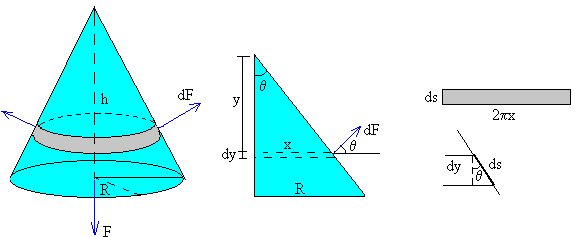
La fuerza dF que ejerce el líquido sobre el elemento de la superficie cónica comprendido entre y y y+dy es el producto de la presión del líquido a la profundidad y, multiplicado por el área de la superficie del tronco de cono de radio x y altura dy. El área de esta superficie es equivalente a la de un rectángulo de longitud 2πx y anchura ds=dy/cosθ.
La fuerza es dF=ρgy·2πxds
La componente vertical de dicha fuerza es
dFy=dF·senθ= ρgy·2πxdy·tanθ
La relación entre x e y y el ángulo θ es
![]()
La componente vertical de la suma de todas las fuerzas que ejerce el líquido sobre los elementos de la superficie lateral del cono es
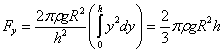
La componente vertical de la resultante de las fuerzas que ejerce el líquido debido a la presión sobre superficie total del cono es
![]()
que está dirigida hacia abajo, y coincide con el peso del fluido.
Como hemos comprobado en estos ejemplos, la paradoja hidrostática consiste en que la fuerza debida a la presión del líquido sobre la base del recipiente puede ser diferente del peso del líquido que lo contiene. Pero esta paradoja se resuelve en el momento en el que tenemos en cuenta las componentes verticales de las fuerzas que ejerce el líquido sobre todas las paredes del recipiente originadas por la la presión.
Referencias
Wilson A. The hydrostatic paradox. The Physics Teacher, Vol. 33, November 1995, pp. 538-539.
Walker J. The hydrostatic paradox: simple geometries, explicit calculations. The Physics Teacher, Vol. 36, September 1998, pp. 378-379.
|
|