Pérdidas continuas
Las pérdidas por rozamientos son función de la rugosidad del conducto, de la viscosidad del fluido, del régimen de funcionamiento (flujo laminar o flujo turbulento) y del caudal circulante, es decir de la velocidad (a más velocidad, más pérdidas).
Si es L la distancia entre los puntos 1 y 2 (medidos a lo largo de la conducción), entonces el cociente (pérdidas (1,2)) / L representa la pérdida de altura por unidad de longitud de la conducción se le llama pendiente de la línea de energía. Denominemosla J
Cuando el flujo es turbulento (número de Reynolds superior a 4.000; 2000<Re< 4000 Es el flujo de transición; 2000>Re Flujo laminar), lo que ocurre en la práctica totalidad de los casos, existen varias fórmulas, tanto teóricas (Ecuación de Darcy-Weisbach), como experimentales (ecuación de Hazen-Williams, ecuación de Manning, etc), que relacionan la pendiente de la línea de energía con la velocidad de circulación del fluido. Quizás la más sencilla y más utilizada sea la fórmula de Manning:

- V = velocidad del agua (m/s)
- K = coeficiente de rugosidad, depende del material de la tubería y del estado de esta. Existen varias expresiones para este coeficiente calculados en forma experimental por varios investigadores como: Manning; Bazin; Kutter; Strickler, entre otros.
- Rh = radio hidráulico de la sección = Área mojada / Perímetro mojado (un cuarto del diámetro para conductos circulares a sección llena) (m)
- J = gradiente de energía (m/m)
La fórmula que se usa comunmente en el curso de mecánica de fluidos en la UCV es la siguiente
Ecuación de Darcy-Weisbach
La ecuación de Darcy-Weisbach es una ecuación ampliamente usada en hidráulica. Permite el cálculo de la pérdida de carga debida a la fricción dentro una tubería.
La ecuación fue inicialmente una variante de la ecuación de Prony, desarrollada por el francés Henry Darcy. En 1845 fue refinada por Julius Weisbach, de Sajonia, hasta la forma en que se conoce actualmente:
donde hf es la pérdida de carga debida a la fricción, calculada a partir de la fricción φ (término este conocido como factor de fricción de Darcy o coeficiente de rozamiento), la relación entre la longitud y el diámetro de la tubería L/D, la velocidad del flujo v, y la aceleración debida a la gravedad g que es constante.
El factor de fricción φ varía de acuerdo a los parámetros de la tubería y la velocidad del flujo, y puede ser conocido con una gran exactitud dentro de ciertos regímenes de flujo. Sin embargo, los datos acerca de su variación con la velocidad eran inicialmente desconocidos, por lo que esta ecuación fue inicialmente superada en muchos casos por la ecuación empírica de Prony.
Años más tarde se evitó su uso en diversos casos especiales en favor de otras ecuaciones empíricas, principalmente la ecuación de Hazen-Williams, ecuaciones que, en la mayoría de los casos, eran significativamente más fáciles de calcular. No obstante, desde la llegada de las calculadoras la facilidad de cálculo no es mayor problema, por lo que la ecuación de Darcy-Weisbach es la preferida.
En en curso de mecánica de fluidos de la UCV comúnmente se usa la ecuación de Colebrook-White para hallar el factor de fricción
Ecuación de Colebrook-White
Fórmula usada en hidráulica para el cálculo del factor de fricción de Darcy λ también conocido como coeficiente de rozamiento. Se trata del mismo factor λ que aparece en la ecuación de Darcy-Weisbach.
La expresión de la fórmula de Colebrook-White es la siguiente:
Donde Re es el número de Reynolds, k / D la rugosidad relativa y λ el factor de fricción.
El campo de aplicación de esta fórmula se encuentra en la zona de transición de flujo laminar a flujo turbulento y flujo turbulento. Para la obtención de λ es necesario el uso de métodos iterativos. Otra forma más sencilla y directa de obtener el valor de λ es hacer uso del diagrama de Moody.
Para el caso particular de tuberías lisas la rugosidad relativa, es decir la relación entre la rugosidad en las paredes de la tubería y el diámetro de la misma, es muy pequeño con lo que el término k / D es muy pequeño y puede despreciarse el primer sumando situado dentro del paréntesis de la ecuación anterior. Quedando en este caso particular la ecuación del siguiente modo:
Para números de Reynolds muy grandes el segundo sumando situado dentro del paréntesis de la ecuación de Colebrook-White es despreciable. En este caso la viscosidad no influye en la práctica a la hora de determinar el coeficiente de fricción, este únicamente depende de la rugosidad relativa k / D de la tubería. Esto se manifiesta en el diagrama de Moody en que en la curva para valores elevados de Re se hacen rectas.
Diagrama de Moody
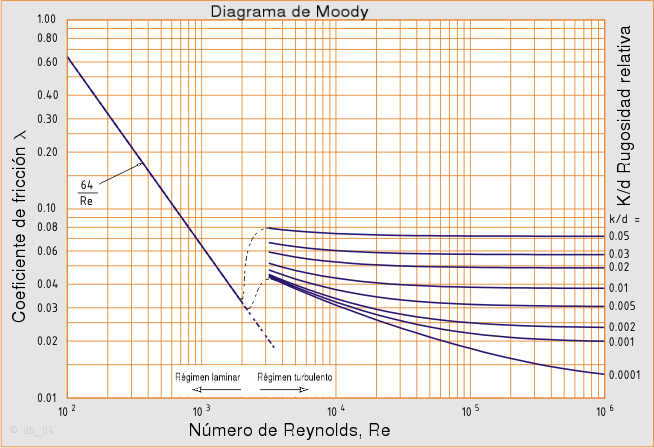
El diagrama de Moody es la representación gráfica en escala doblemente logarítmica del factor de fricción en función del número de Reynolds y la rugosidad relativa de una tubería.
En la ecuación de Darcy-Weisbach aparece el término λ que representa el factor de fricción de Darcy, conocido también como coeficiente de fricción. El cálculo de este coeficiente no es inmediato y no existe una única fórmula para calcularlo en todas las situaciones posibles.
Se pueden distinguir dos situaciones diferentes, el caso en que el flujo sea laminar y el caso en que el flujo sea turbulento. En el caso de flujo laminar se usa una de las expresiones de la ecuación de Poiseuille; en el caso de flujo turbulento se usa la ecuación de Colebrook-White.
En el caso de flujo laminar el factor de fricción depende únicamente del número de Reynolds. Para flujo turbulento, el factor de fricción depende tanto del número de Reynolds como de la rugosidad relativa de la tubería, por eso en este caso se representa mediante una familia de curvas, una para cada valor del parámetro k / D, donde k es el valor de la rugosidad absoluta, es decir la longitud (habitualmente en milímetros) de la rugosidad directamente medible en la tubería.
En la siguiente imagen se puede observar el aspecto del diagrama de Moody.
|
|